Static_pages




A wave equation, involving Chirality and such

===============================

Source Code

===============================



import math


def finding_chirality(n):

  for a in range(1, n):

    aaa = (a * a * a);

    for b in range(1, n):

      c = math.sqrt(aaa + (b * b * b))

      if c % 1 == 0:

        print("[ %d %d  %d ] { %d\u00b3 + %d\u00b3 = %d\u00b2 }" % (a, b, c, a,b,c))


def finding_chirality_specific(a, n):

    aaa = (a * a * a);

    for b in range(1, n):

      c = math.sqrt(aaa + (b * b * b))

      if c % 1 == 0:

        print("[ %d %d  %d ] { %d\u00b3 + %d\u00b3 = %d\u00b2 }" % (a, b, c, a,b,c))


finding_chirality(137)

===============================

results


[ 1 2  3 ] { 1³ + 2³ = 3² }

[ 2 1  3 ] { 2³ + 1³ = 3² }

[ 2 2  4 ] { 2³ + 2³ = 4² }

[ 2 46  312 ] { 2³ + 46³ = 312² }

[ 4 8  24 ] { 4³ + 8³ = 24² }

[ 7 21  98 ] { 7³ + 21³ = 98² }

[ 8 4  24 ] { 8³ + 4³ = 24² }

[ 8 8  32 ] { 8³ + 8³ = 32² }

[ 9 18  81 ] { 9³ + 18³ = 81² }

[ 10 65  525 ] { 10³ + 65³ = 525² }

[ 11 37  228 ] { 11³ + 37³ = 228² }

[ 14 70  588 ] { 14³ + 70³ = 588² }

[ 16 32  192 ] { 16³ + 32³ = 192² }

[ 18 9  81 ] { 18³ + 9³ = 81² }

[ 18 18  108 ] { 18³ + 18³ = 108² }

[ 21 7  98 ] { 21³ + 7³ = 98² }

[ 22 26  168 ] { 22³ + 26³ = 168² }

[ 25 50  375 ] { 25³ + 50³ = 375² }

[ 26 22  168 ] { 26³ + 22³ = 168² }

[ 28 84  784 ] { 28³ + 84³ = 784² }

[ 32 16  192 ] { 32³ + 16³ = 192² }

[ 32 32  256 ] { 32³ + 32³ = 256² }

[ 33 88  847 ] { 33³ + 88³ = 847² }

[ 36 72  648 ] { 36³ + 72³ = 648² }

[ 37 11  228 ] { 37³ + 11³ = 228² }

[ 46 2  312 ] { 46³ + 2³ = 312² }

[ 49 98  1029 ] { 49³ + 98³ = 1029² }

[ 50 25  375 ] { 50³ + 25³ = 375² }

[ 50 50  500 ] { 50³ + 50³ = 500² }

[ 56 65  671 ] { 56³ + 65³ = 671² }

[ 57 112  1261 ] { 57³ + 112³ = 1261² }

[ 64 128  1536 ] { 64³ + 128³ = 1536² }

[ 65 10  525 ] { 65³ + 10³ = 525² }

[ 65 56  671 ] { 65³ + 56³ = 671² }

[ 65 91  1014 ] { 65³ + 91³ = 1014² }

[ 65 104  1183 ] { 65³ + 104³ = 1183² }

[ 70 14  588 ] { 70³ + 14³ = 588² }

[ 70 105  1225 ] { 70³ + 105³ = 1225² }

[ 72 36  648 ] { 72³ + 36³ = 648² }

[ 72 72  864 ] { 72³ + 72³ = 864² }

[ 84 28  784 ] { 84³ + 28³ = 784² }

[ 84 105  1323 ] { 84³ + 105³ = 1323² }

[ 88 33  847 ] { 88³ + 33³ = 847² }

[ 88 104  1344 ] { 88³ + 104³ = 1344² }

[ 91 65  1014 ] { 91³ + 65³ = 1014² }

[ 98 49  1029 ] { 98³ + 49³ = 1029² }

[ 98 98  1372 ] { 98³ + 98³ = 1372² }

[ 104 65  1183 ] { 104³ + 65³ = 1183² }

[ 104 88  1344 ] { 104³ + 88³ = 1344² }

[ 105 70  1225 ] { 105³ + 70³ = 1225² }

[ 105 84  1323 ] { 105³ + 84³ = 1323² }

[ 112 57  1261 ] { 112³ + 57³ = 1261² }

[ 128 64  1536 ] { 128³ + 64³ = 1536² }

[ 128 128  2048 ] { 128³ + 128³ = 2048² }


===============================

===============================



relevant paper;


===============================

also =>  a different cubic construct code

===============================

and including some results with source code:


import math

def finding_chirality_isomerism (n):

  for b in range(n):

    for a in range(1, b):

      c = math.sqrt(( a * a * a ) + (b * b * b))

      if c % 1 == 0:

        print("[ %d %d  %d ] { %d\u00b3 + %d\u00b3 = %d\u00b2 }" % (a, b, c, a,b,c))


finding_chirality_isomerism (3200)

================================================

sort -n -k 2  results_chirality2.txt > results_chirality2_sorted.txt 

================================================



https://arstechnica.com/science/2022/02/latest-success-from-googles-ai-group-controlling-a-fusion-reactor/

Latest success from Google’s AI group: Controlling a fusion reactor
The AI was trained on a simulator to shape the plasma held within a tokamak.
"  During training, an intervening layer of software provided a reward function that indicated how close the plasma's properties were to the desired state. Another algorithm, termed a "critic," learned the expected rewards for various changes to the tokamak's control magnets. These were used by the actual control neural network to learn which actions it should take.

The critic was elaborate and computationally expensive, but it was only used during the training portion. When training was done, the control algorithm had learned which actions to take to reach a variety of states, and the critic could be discarded.  "


[ 1 2  3 ] { 1³ + 2³ = 3² }

[ 2 46  312 ] { 2³ + 46³ = 312² }

[ 4 8  24 ] { 4³ + 8³ = 24² }

[ 7 21  98 ] { 7³ + 21³ = 98² }

[ 8 184  2496 ] { 8³ + 184³ = 2496² }

[ 9 18  81 ] { 9³ + 18³ = 81² }

[ 10 65  525 ] { 10³ + 65³ = 525² }

[ 11 37  228 ] { 11³ + 37³ = 228² }

[ 14 70  588 ] { 14³ + 70³ = 588² }

[ 16 32  192 ] { 16³ + 32³ = 192² }

[ 18 414  8424 ] { 18³ + 414³ = 8424² }

[ 22 26  168 ] { 22³ + 26³ = 168² }

[ 23 1177  40380 ] { 23³ + 1177³ = 40380² }

[ 25 50  375 ] { 25³ + 50³ = 375² }

[ 28 84  784 ] { 28³ + 84³ = 784² }

[ 32 736  19968 ] { 32³ + 736³ = 19968² }

[ 33 88  847 ] { 33³ + 88³ = 847² }

[ 34 450  9548 ] { 34³ + 450³ = 9548² }

[ 35 665  17150 ] { 35³ + 665³ = 17150² }

[ 36 72  648 ] { 36³ + 72³ = 648² }

[ 37 407  8214 ] { 37³ + 407³ = 8214² }

[ 38 1178  40432 ] { 38³ + 1178³ = 40432² }

[ 40 260  4200 ] { 40³ + 260³ = 4200² }

[ 44 148  1824 ] { 44³ + 148³ = 1824² }

[ 49 98  1029 ] { 49³ + 98³ = 1029² }

[ 50 1150  39000 ] { 50³ + 1150³ = 39000² }

[ 56 280  4704 ] { 56³ + 280³ = 4704² }

[ 56 65  671 ] { 56³ + 65³ = 671² }

[ 57 112  1261 ] { 57³ + 112³ = 1261² }

[ 57 456  9747 ] { 57³ + 456³ = 9747² }

[ 63 189  2646 ] { 63³ + 189³ = 2646² }

[ 64 128  1536 ] { 64³ + 128³ = 1536² }

[ 65 104  1183 ] { 65³ + 104³ = 1183² }

[ 65 260  4225 ] { 65³ + 260³ = 4225² }

[ 65 610  15075 ] { 65³ + 610³ = 15075² }

[ 65 91  1014 ] { 65³ + 91³ = 1014² }

[ 70 105  1225 ] { 70³ + 105³ = 1225² }

[ 72 1656  67392 ] { 72³ + 1656³ = 67392² }

[ 78 273  4563 ] { 78³ + 273³ = 4563² }

[ 78 354  6696 ] { 78³ + 354³ = 6696² }

[ 81 162  2187 ] { 81³ + 162³ = 2187² }

[ 84 105  1323 ] { 84³ + 105³ = 1323² }

[ 86 602  14792 ] { 86³ + 602³ = 14792² }

[ 88 104  1344 ] { 88³ + 104³ = 1344² }

[ 90 585  14175 ] { 90³ + 585³ = 14175² }

[ 95 1121  37544 ] { 95³ + 1121³ = 37544² }

[ 98 2254  107016 ] { 98³ + 2254³ = 107016² }

[ 99 333  6156 ] { 99³ + 333³ = 6156² }

[ 100 200  3000 ] { 100³ + 200³ = 3000² }

[ 112 336  6272 ] { 112³ + 336³ = 6272² }

[ 114 190  2888 ] { 114³ + 190³ = 2888² }

[ 121 242  3993 ] { 121³ + 242³ = 3993² }

[ 122 1201  41643 ] { 122³ + 1201³ = 41643² }

[ 126 630  15876 ] { 126³ + 630³ = 15876² }

[ 128 2944  159744 ] { 128³ + 2944³ = 159744² }

[ 130 546  12844 ] { 130³ + 546³ = 12844² }

[ 132 352  6776 ] { 132³ + 352³ = 6776² }

[ 136 1800  76384 ] { 136³ + 1800³ = 76384² }

[ 140 2660  137200 ] { 140³ + 2660³ = 137200² }

[ 144 288  5184 ] { 144³ + 288³ = 5184² }

[ 148 1628  65712 ] { 148³ + 1628³ = 65712² }

[ 154 330  6292 ] { 154³ + 330³ = 6292² }

[ 160 1040  33600 ] { 160³ + 1040³ = 33600² }

[ 169 338  6591 ] { 169³ + 338³ = 6591² }

[ 170 506  11596 ] { 170³ + 506³ = 11596² }

[ 175 525  12250 ] { 175³ + 525³ = 12250² }

[ 176 592  14592 ] { 176³ + 592³ = 14592² }

[ 177 1551  61128 ] { 177³ + 1551³ = 61128² }

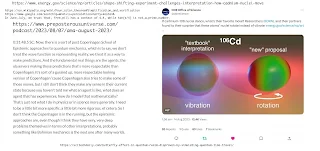
propagation_of_torque,
through Hilbert space

[ 183 249  4644 ] { 183³ + 249³ = 4644² }

[ 184 345  6877 ] { 184³ + 345³ = 6877² }

[ 196 392  8232 ] { 196³ + 392³ = 8232² }

[ 198 234  4536 ] { 198³ + 234³ = 4536² }

[ 211 3165  178084 ] { 211³ + 3165³ = 178084² }

[ 217 1302  47089 ] { 217³ + 1302³ = 47089² }

[ 217 312  6371 ] { 217³ + 312³ = 6371² }

[ 224 1120  37632 ] { 224³ + 1120³ = 37632² }

[ 224 260  5368 ] { 224³ + 260³ = 5368² }

[ 225 450  10125 ] { 225³ + 450³ = 10125² }

[ 228 1824  77976 ] { 228³ + 1824³ = 77976² }

[ 228 448  10088 ] { 228³ + 448³ = 10088² }

[ 238 518  12348 ] { 238³ + 518³ = 12348² }

[ 242 433  9765 ] { 242³ + 433³ = 9765² }

[ 247 1157  39546 ] { 247³ + 1157³ = 39546² }

[ 250 1625  65625 ] { 250³ + 1625³ = 65625² }

[ 252 756  21168 ] { 252³ + 756³ = 21168² }

[ 256 512  12288 ] { 256³ + 512³ = 12288² }

[ 259 2093  95844 ] { 259³ + 2093³ = 95844² }

[ 260 1040  33800 ] { 260³ + 1040³ = 33800² }

[ 260 2440  120600 ] { 260³ + 2440³ = 120600² }

[ 260 364  8112 ] { 260³ + 364³ = 8112² }

[ 260 416  9464 ] { 260³ + 416³ = 9464² }

[ 266 665  17689 ] { 266³ + 665³ = 17689² }

[ 273 364  8281 ] { 273³ + 364³ = 8281² }

[ 275 925  28500 ] { 275³ + 925³ = 28500² }

[ 280 420  9800 ] { 280³ + 420³ = 9800² }

[ 289 578  14739 ] { 289³ + 578³ = 14739² }

[ 297 792  22869 ] { 297³ + 792³ = 22869² }

[ 304 1121  37905 ] { 304³ + 1121³ = 37905² }

[ 305 1064  35113 ] { 305³ + 1064³ = 35113² }

[ 305 895  27300 ] { 305³ + 895³ = 27300² }

[ 312 1092  36504 ] { 312³ + 1092³ = 36504² }

[ 312 1416  53568 ] { 312³ + 1416³ = 53568² }

[ 322 1001  32193 ] { 322³ + 1001³ = 32193² }

[ 324 648  17496 ] { 324³ + 648³ = 17496² }

[ 329 1880  81733 ] { 329³ + 1880³ = 81733² }

[ 329 371  9310 ] { 329³ + 371³ = 9310² }

[ 330 1786  75716 ] { 330³ + 1786³ = 75716² }

[ 330 345  8775 ] { 330³ + 345³ = 8775² }

[ 336 420  10584 ] { 336³ + 420³ = 10584² }

[ 343 1029  33614 ] { 343³ + 1029³ = 33614² }

[ 344 2408  118336 ] { 344³ + 2408³ = 118336² }

[ 350 1750  73500 ] { 350³ + 1750³ = 73500² }

[ 352 416  10752 ] { 352³ + 416³ = 10752² }

[ 360 2340  113400 ] { 360³ + 2340³ = 113400² }

[ 361 722  20577 ] { 361³ + 722³ = 20577² }

[ 396 1332  49248 ] { 396³ + 1332³ = 49248² }

[ 400 800  24000 ] { 400³ + 800³ = 24000² }

[ 417 1807  77284 ] { 417³ + 1807³ = 77284² }

[ 441 882  27783 ] { 441³ + 882³ = 27783² }

[ 448 1344  50176 ] { 448³ + 1344³ = 50176² }

[ 455 1001  33124 ] { 455³ + 1001³ = 33124² }

[ 456 760  23104 ] { 456³ + 760³ = 23104² }

[ 469 603  17956 ] { 469³ + 603³ = 17956² }

[ 470 730  22200 ] { 470³ + 730³ = 22200² }

[ 484 968  31944 ] { 484³ + 968³ = 31944² }

[ 485 715  21900 ] { 485³ + 715³ = 21900² }

[ 490 3185  180075 ] { 490³ + 3185³ = 180075² }

[ 504 2520  127008 ] { 504³ + 2520³ = 127008² }

[ 504 585  18117 ] { 504³ + 585³ = 18117² }

[ 506 1222  44208 ] { 506³ + 1222³ = 44208² }

[ 506 1610  65596 ] { 506³ + 1610³ = 65596² }

[ 513 1008  34047 ] { 513³ + 1008³ = 34047² }

[ 520 2184  102752 ] { 520³ + 2184³ = 102752² }

[ 528 1408  54208 ] { 528³ + 1408³ = 54208² }

[ 529 1058  36501 ] { 529³ + 1058³ = 36501² }

[ 539 1813  78204 ] { 539³ + 1813³ = 78204² }

[ 546 777  25137 ] { 546³ + 777³ = 25137² }

[ 550 650  21000 ] { 550³ + 650³ = 21000² }

[ 553 1148  41013 ] { 553³ + 1148³ = 41013² }

[ 559 2193  103544 ] { 559³ + 2193³ = 103544² }

[ 567 1701  71442 ] { 567³ + 1701³ = 71442² }

[ 576 1152  41472 ] { 576³ + 1152³ = 41472² }

[ 585 2340  114075 ] { 585³ + 2340³ = 114075² }

[ 585 819  27378 ] { 585³ + 819³ = 27378² }

[ 585 936  31941 ] { 585³ + 936³ = 31941² }

[ 592 1617  66599 ] { 592³ + 1617³ = 66599² }

[ 592 777  26011 ] { 592³ + 777³ = 26011² }

[ 598 702  23660 ] { 598³ + 702³ = 23660² }

[ 616 1320  50336 ] { 616³ + 1320³ = 50336² }

[ 620 1705  72075 ] { 620³ + 1705³ = 72075² }

[ 625 1250  46875 ] { 625³ + 1250³ = 46875² }

[ 630 945  33075 ] { 630³ + 945³ = 33075² }

[ 642 1086  39312 ] { 642³ + 1086³ = 39312² }

[ 658 1694  71736 ] { 658³ + 1694³ = 71736² }

[ 665 2926  159201 ] { 665³ + 2926³ = 159201² }

[ 665 760  27075 ] { 665³ + 760³ = 27075² }

[ 676 1352  52728 ] { 676³ + 1352³ = 52728² }

[ 680 2024  92768 ] { 680³ + 2024³ = 92768² }

[ 700 2100  98000 ] { 700³ + 2100³ = 98000² }

[ 702 2457  123201 ] { 702³ + 2457³ = 123201² }

[ 702 3186  180792 ] { 702³ + 3186³ = 180792² }

[ 704 2368  116736 ] { 704³ + 2368³ = 116736² }

[ 721 1302  50813 ] { 721³ + 1302³ = 50813² }

[ 721 2060  95481 ] { 721³ + 2060³ = 95481² }

[ 728 1729  74529 ] { 728³ + 1729³ = 74529² }

[ 729 1458  59049 ] { 729³ + 1458³ = 59049² }

[ 730 1241  47961 ] { 730³ + 1241³ = 47961² }

[ 732 996  37152 ] { 732³ + 996³ = 37152² }

[ 736 1380  55016 ] { 736³ + 1380³ = 55016² }

[ 737 1072  40401 ] { 737³ + 1072³ = 40401² }

[ 756 945  35721 ] { 756³ + 945³ = 35721² }

[ 770 2905  158025 ] { 770³ + 2905³ = 158025² }

[ 784 1568  65856 ] { 784³ + 1568³ = 65856² }

[ 792 936  36288 ] { 792³ + 936³ = 36288² }

[ 793 2928  160003 ] { 793³ + 2928³ = 160003² }

[ 793 854  33489 ] { 793³ + 854³ = 33489² }

[ 825 2200  105875 ] { 825³ + 2200³ = 105875² }

[ 841 1682  73167 ] { 841³ + 1682³ = 73167² }

[ 847 2541  130438 ] { 847³ + 2541³ = 130438² }

[ 851 877  35928 ] { 851³ + 877³ = 35928² }

[ 858 2409  120879 ] { 858³ + 2409³ = 120879² }

[ 868 1248  50968 ] { 868³ + 1248³ = 50968² }

[ 891 2997  166212 ] { 891³ + 2997³ = 166212² }

[ 896 1040  42944 ] { 896³ + 1040³ = 42944² }

[ 900 1800  81000 ] { 900³ + 1800³ = 81000² }

[ 912 1792  80704 ] { 912³ + 1792³ = 80704² }

[ 925 3071  172494 ] { 925³ + 3071³ = 172494² }

[ 952 2072  98784 ] { 952³ + 2072³ = 98784² }

[ 961 1922  89373 ] { 961³ + 1922³ = 89373² }

[ 968 1732  78120 ] { 968³ + 1732³ = 78120² }

[ 1001 2480  127499 ] { 1001³ + 2480³ = 127499² }

[ 1001 2674  141855 ] { 1001³ + 2674³ = 141855² }

[ 1008 3024  169344 ] { 1008³ + 3024³ = 169344² }

[ 1022 2482  127896 ] { 1022³ + 2482³ = 127896² }

[ 1024 2048  98304 ] { 1024³ + 2048³ = 98304² }

[ 1026 1710  77976 ] { 1026³ + 1710³ = 77976² }

[ 1040 1456  64896 ] { 1040³ + 1456³ = 64896² }

[ 1040 1664  75712 ] { 1040³ + 1664³ = 75712² }

[ 1064 2660  141512 ] { 1064³ + 2660³ = 141512² }

[ 1078 1274  57624 ] { 1078³ + 1274³ = 57624² }

[ 1089 2178  107811 ] { 1089³ + 2178³ = 107811² }

[ 1092 1456  66248 ] { 1092³ + 1456³ = 66248² }

[ 1110 2590  136900 ] { 1110³ + 2590³ = 136900² }

[ 1120 1680  78400 ] { 1120³ + 1680³ = 78400² }

[ 1156 2312  117912 ] { 1156³ + 2312³ = 117912² }

[ 1169 1183  57036 ] { 1169³ + 1183³ = 57036² }

[ 1188 3168  182952 ] { 1188³ + 3168³ = 182952² }

[ 1209 1950  95823 ] { 1209³ + 1950³ = 95823² }

[ 1225 2450  128625 ] { 1225³ + 2450³ = 128625² }

[ 1296 2592  139968 ] { 1296³ + 2592³ = 139968² }

[ 1298 1969  99099 ] { 1298³ + 1969³ = 99099² }

[ 1302 2046  103788 ] { 1302³ + 2046³ = 103788² }

[ 1316 1484  74480 ] { 1316³ + 1484³ = 74480² }

[ 1320 1380  70200 ] { 1320³ + 1380³ = 70200² }

[ 1344 1680  84672 ] { 1344³ + 1680³ = 84672² }

[ 1369 2738  151959 ] { 1369³ + 2738³ = 151959² }

[ 1376 2345  124501 ] { 1376³ + 2345³ = 124501² }

[ 1386 2970  169884 ] { 1386³ + 2970³ = 169884² }

[ 1400 1625  83875 ] { 1400³ + 1625³ = 83875² }

[ 1408 1664  86016 ] { 1408³ + 1664³ = 86016² }

[ 1416 2065  107911 ] { 1416³ + 2065³ = 107911² }

[ 1425 2800  157625 ] { 1425³ + 2800³ = 157625² }

[ 1444 2888  164616 ] { 1444³ + 2888³ = 164616² }

[ 1521 3042  177957 ] { 1521³ + 3042³ = 177957² }

[ 1610 2065  113925 ] { 1610³ + 2065³ = 113925² }

[ 1625 2275  126750 ] { 1625³ + 2275³ = 126750² }

[ 1625 2600  147875 ] { 1625³ + 2600³ = 147875² }

[ 1628 2849  165649 ] { 1628³ + 2849³ = 165649² }

[ 1647 2241  125388 ] { 1647³ + 2241³ = 125388² }

[ 1656 3105  185679 ] { 1656³ + 3105³ = 185679² }

[ 1705 2046  116281 ] { 1705³ + 2046³ = 116281² }

[ 1706 1969  112245 ] { 1706³ + 1969³ = 112245² }

[ 1737 3088  186245 ] { 1737³ + 3088³ = 186245² }

[ 1750 2625  153125 ] { 1750³ + 2625³ = 153125² }

[ 1782 2106  122472 ] { 1782³ + 2106³ = 122472² }

[ 1793 2282  132845 ] { 1793³ + 2282³ = 132845² }

[ 1824 3040  184832 ] { 1824³ + 3040³ = 184832² }

[ 1876 2412  143648 ] { 1876³ + 2412³ = 143648² }

[ 1880 2920  177600 ] { 1880³ + 2920³ = 177600² }

[ 1884 2041  123245 ] { 1884³ + 2041³ = 123245² }

[ 1940 2860  175200 ] { 1940³ + 2860³ = 175200² }

[ 1953 2808  172017 ] { 1953³ + 2808³ = 172017² }

[ 1957 2907  179056 ] { 1957³ + 2907³ = 179056² }

[ 1960 3081  191771 ] { 1960³ + 3081³ = 191771² }

[ 2016 2340  144936 ] { 2016³ + 2340³ = 144936² }

[ 2041 2522  156663 ] { 2041³ + 2522³ = 156663² }

[ 2100 2625  165375 ] { 2100³ + 2625³ = 165375² }

[ 2184 3108  201096 ] { 2184³ + 3108³ = 201096² }

[ 2200 2600  168000 ] { 2200³ + 2600³ = 168000² }

[ 2257 2543  167160 ] { 2257³ + 2543³ = 167160² }

[ 2290 2510  166800 ] { 2290³ + 2510³ = 166800² }

[ 2368 3108  208088 ] { 2368³ + 3108³ = 208088² }

[ 2392 2808  189280 ] { 2392³ + 2808³ = 189280² }

[ 2409 2920  197173 ] { 2409³ + 2920³ = 197173² }

[ 2590 2849  201243 ] { 2590³ + 2849³ = 201243² }

[ 2660 3040  216600 ] { 2660³ + 3040³ = 216600² }

[ 2662 3146  223608 ] { 2662³ + 3146³ = 223608² }

[ 2744 3185  230153 ] { 2744³ + 3185³ = 230153² }

[ 2970 3105  236925 ] { 2970³ + 3105³ = 236925² }



===============================

===============================